Social network death spiral: How Metcalfe’s Law can work against you
Metcalfe’s Law
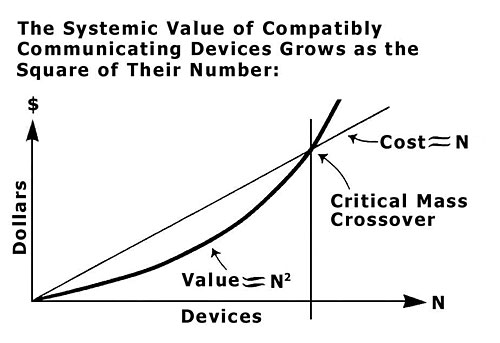
Does everyone remember Metcalfe’s Law? It was formulated by Bob Metcalfe, the inventor of Ethernet and co-founder of 3Com, who stated:
The value of a network is proportional to the square of the number of users of the system (n²).
For those that are interested in the math behind it, basically the idea is that if every new node in the network connects with every pre-existing node, then as you gain nodes, you non-linearly increase the number of connections that everyone has with everyone else.
That’s pretty neat, and for the social networking folks who are aggregating large audiences and treating their businesses like communication utilities, it’s both logical and helpful to think that these social communities abide by network effects like Metcalfe’s Law. In fact, it’s a DIRECT reason why these networks want to get as big as possible, and have a social graph that’s as comprehensive as possible, and why they should ultimately be opposed to Data Portability. And I think we’ll see these players’ strategies ultimately reflect these strategies.
But Metcalfe’s Law can also affect social app creators. Let’s discuss how this might play out for folks who are building apps on social platforms, rather than operating the social platforms themselves:
“Jumping the shark” and Metcalfe’s Law
In a previous post, I wrote a bunch about how dangerous (and easy) it is to jump the shark in an enclosed space like the Facebook Platform.
Here’s the good scenario:
Let’s say that you retain users well, and you don’t get a sharkfin graph on your traffic. In that case, if you combine the two ideas – Metcalfe’s Law and with the viral loops on the social platforms – you can imagine that in the success case, you are creating N^2 value with very large N.
For folks building application on Facebook, Opensocial, etc., it’s nice to think that your new app is gaining value much faster than if you built your own
destination site. This allows you to get the N^2 benefits of Metcalfe’s Law without incurring significant costs of acquisition as you scale N up to a large number. This the best of both worlds.
Here’s the bad scenario:
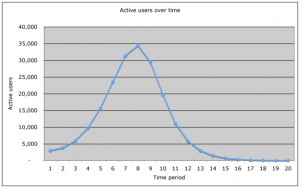
Let’s consider the other case, where your app’s retention sucks, and you are going through the sharkfin graph of rapidly acquiring users, hitting a peak, and then falling down:
(scroll past the image for more)
Now all of a sudden, Metcalfe’s Law works against you – for this, I will introduce the corollary, Eflactem’s Law.
Eflactem’s Law
Funny enough, everyone always talks about Metcalfe’s Law like it’s a good thing, and they say that because they assume that N is increasing! But let’s consider the opposite: If Metcalfe’s Law says that your network grows value competed by N^2, then Eflactem’s Law states the reverse. It says:
As you lose users, the value of your network is decreases exponentially (doh!)
That is:
- If you have 100 users, and then grow to 200 users, your “value” has increased from 10k to 40k.
- But if you START with 200 users, and end up with 100, then you are going from 40k in value to 10k in value.
And that sucks. Perhaps this should be called Murphy’s Law instead?
In fact, you see this happen all the time at dinner parties or events. Things are great until one or two people announce the intention to leave. If those folks are fun and entertaining, there’s an immediate realization that the quality of the experience is about to go down. And yet more people announce their intention to leave, and so on, until you are left with the party hosts and a big mess ;-)
Advanced discussion: Social Network Death Spiral
Now let’s do a more advanced discussion using the concepts above – for some new readers, this discussion might completely be incoherent ;-)
Let’s consider a specific scenario where a social network could easily start to “Death Spiral” – here’s some set up on the scenario:
- You have a bunch of users, let’s call the total number N
- The total number of users in the ecosystem, called the carrying capacity, is variable C
- These users all individually require some utility value on a site, let’s call this V_required
- Then there’s a retention %, called R, which depends on two factors:
- If the utility value for users is satisfied, that is, V > V_required, then R close to 100%
- If the utility value drops under V_required, then R is crappy, closer to 0%
- And to borrow Metcalfe’s Law, the value of the network is calculated at V = N^2
So the scenario is that as the total users for the application reaches the carrying capacity, you basically hit a point of maximum saturation – this is defined by the ratio N/C. Sometimes this ratio can also be referred to as the “efficiency” of a user acquisition process, which relays how many people you actually acquire versus the universe of all users. (Obviously you want this to be as large as possible)
Once you hit the carrying capacity and acquire all possible users, N is at the highest point, and thus the network value is also at its highest point, V = N_max^2. Similarly, because the network value V is at its highest, the retention reaches its highest point as well.
The question in this scenario is, at any point during the growth of the network, does the network value V exceed the required value of the site, which we call V_required? Does the network break through the critical mass of value?
If so, retention should be great, as defined by the explanation above. In fact, maybe you reach V_required early on during the growth of the site, which makes the acquisition process much more efficient. Early on, maybe the userbase wasn’t sticking, but a critical mass threshold is met, and suddenly the entire userbase sticks, which creates a long-term creation of ad impressions and company value.
However, if you don’t reach the required value in the network, then you’re pretty much screwed. Then the retention sucks, since the users aren’t finding value, and some percentage of them will leave. This will then remove more value from the system, causing yet another round of users to leave. This continual loss of users is a death spiral that collapses your network in fine Eflactem’s Law style.
A very interesting variation of this is when you apply Metcalfe’s Law not to the entire network of users, but rather think of a social network as a loosely grouped set of connections. In that case, some local networks might have achieved critical mass, and if they are big enough, they will be retained. However, if the smaller networks around any given group start collapsing, then sometimes even the large networks will get pulled down with them.
Conclusion
To summarize this post:
- Gaining users is great, but preventing the loss of users is also very important
- Creating a sharkfin graph on your traffic means exponential descruction of value
- Critical mass plus network effects implies that complete collapse of networks is possible too
As always, comments and questions are welcome.
PS. Get new updates/analysis on tech and startupsI write a high-quality, weekly newsletter covering what's happening in Silicon Valley, focused on startups, marketing, and mobile.
Views expressed in “content” (including posts, podcasts, videos) linked on this website or posted in social media and other platforms (collectively, “content distribution outlets”) are my own and are not the views of AH Capital Management, L.L.C. (“a16z”) or its respective affiliates. AH Capital Management is an investment adviser registered with the Securities and Exchange Commission. Registration as an investment adviser does not imply any special skill or training. The posts are not directed to any investors or potential investors, and do not constitute an offer to sell -- or a solicitation of an offer to buy -- any securities, and may not be used or relied upon in evaluating the merits of any investment.
The content should not be construed as or relied upon in any manner as investment, legal, tax, or other advice. You should consult your own advisers as to legal, business, tax, and other related matters concerning any investment. Any projections, estimates, forecasts, targets, prospects and/or opinions expressed in these materials are subject to change without notice and may differ or be contrary to opinions expressed by others. Any charts provided here are for informational purposes only, and should not be relied upon when making any investment decision. Certain information contained in here has been obtained from third-party sources. While taken from sources believed to be reliable, I have not independently verified such information and makes no representations about the enduring accuracy of the information or its appropriateness for a given situation. The content speaks only as of the date indicated.
Under no circumstances should any posts or other information provided on this website -- or on associated content distribution outlets -- be construed as an offer soliciting the purchase or sale of any security or interest in any pooled investment vehicle sponsored, discussed, or mentioned by a16z personnel. Nor should it be construed as an offer to provide investment advisory services; an offer to invest in an a16z-managed pooled investment vehicle will be made separately and only by means of the confidential offering documents of the specific pooled investment vehicles -- which should be read in their entirety, and only to those who, among other requirements, meet certain qualifications under federal securities laws. Such investors, defined as accredited investors and qualified purchasers, are generally deemed capable of evaluating the merits and risks of prospective investments and financial matters. There can be no assurances that a16z’s investment objectives will be achieved or investment strategies will be successful. Any investment in a vehicle managed by a16z involves a high degree of risk including the risk that the entire amount invested is lost. Any investments or portfolio companies mentioned, referred to, or described are not representative of all investments in vehicles managed by a16z and there can be no assurance that the investments will be profitable or that other investments made in the future will have similar characteristics or results. A list of investments made by funds managed by a16z is available at https://a16z.com/investments/. Excluded from this list are investments for which the issuer has not provided permission for a16z to disclose publicly as well as unannounced investments in publicly traded digital assets. Past results of Andreessen Horowitz’s investments, pooled investment vehicles, or investment strategies are not necessarily indicative of future results. Please see https://a16z.com/disclosures for additional important information.